Wissen
Was ist eigentlich das Delta?
Im Beitrag der Wissensrubrik der vergangenen Ausgabe des ideas-Magazins haben wir Ihnen die verschiedenen Preiseinflussfaktoren und ihre Auswirkungen auf Optionsscheine vorgestellt. Darin wurde unter anderem der Einfluss des Basiswertpreises behandelt. Zur Erinnerung: Je höher der Preis des Basiswerts, umso höher der Preis eines Call Optionsscheins. Bei einem Put Optionsschein verhält es sich genau umgekehrt. Doch professionelle Händler sowie Privatanleger interessiert häufig noch viel mehr, sie möchten eine Aussage über die Stärke der möglichen Preisveränderungen eines Optionsscheins. Hier kommt das »Delta« ins Spiel.
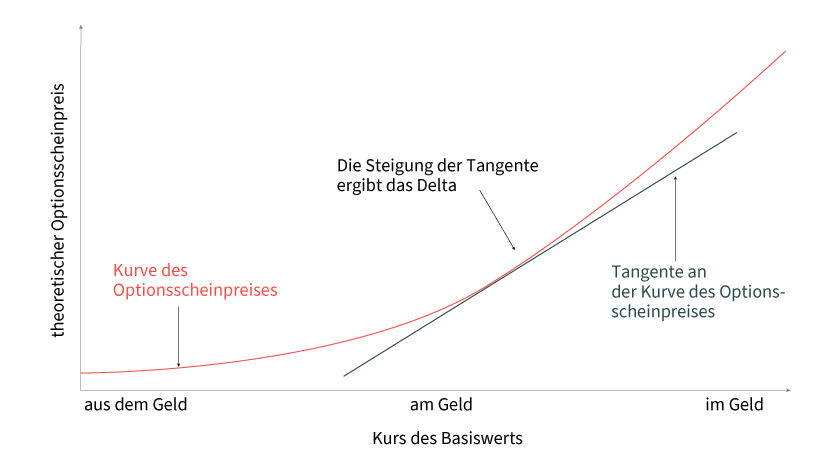
Das Delta ist eine der wichtigsten sogenannten Sensitivitätskennzahlen. Es zeigt die Veränderung des theoretischen Optionsscheinpreises (bereinigt um das Bezugsverhältnis) bei einer Veränderung des Basiswertkurses um eine Einheit. Mathematisch ausgedrückt ist das Delta die erste partielle Ableitung der Optionspreisformel nach dem Kurs des Basiswerts. Stellt man die Kennzahl grafisch dar, so zeigt sie die Steigung der theoretischen Optionsscheinpreiskurve zum jeweils betrachteten Zeitpunkt (siehe Grafik 1).
Das Delta liegt bei klassischen Kaufoptionsscheinen (auch Plain-Vanilla Calls genannt) zwischen 0 und 1, bei Verkaufsoptionsscheinen (Puts) dagegen zwischen 0 und –1. Wobei bei beiden Typen die Höhe des Deltas stark von der sogenannten Moneyness abhängt, präziser, ob der Schein einen inneren Wert hat oder nicht. Je höher der innere Wert, also je tiefer der Kauf- bzw. Verkaufsoptionsschein »im Geld« ist, desto näher liegt sein Delta-Wert an 1 (Call) bzw. –1 (Put). Dabei wird deutlich, dass die Kennzahl Delta keine statische Größe ist, sondern sich mit Änderungen des Basiswertkurses ebenfalls ändert. Ein Kursanstieg des Basiswerts vergrößert das Delta des Call Optionsscheins, ein Kursrückgang dagegen verringert sein Delta. Ein Delta von beispielsweise 0,6 bedeutet bei einem Bezugsverhältnis von 1:1: Steigt der Basiswert um eine Einheit, steigt der Kurs des Call Optionsscheins um 0,6 Einheiten. Put Optionsscheine reagieren bei einer Kurssteigerung des Basiswerts mit einem Preisrückgang, das erklärt das negative Vorzeichen beim Delta eines solchen Optionsscheins.
Beispiel:
Ein Put Optionsschein auf die ABC-Aktie (Bezugsverhältnis von 10:1, das heißt, zehn Optionsscheine beziehen sich auf eine ABC-Aktie) ist leicht im Geld und kostet 0,42 Euro, die Restlaufzeit beträgt sechs Wochen. Das Delta wird auf der Homepage von Société Générale mit –0,7 angegeben. Der Kurs der ABC-Aktie liegt bei 95 Euro und steigt um 1 Euro auf 96 Euro. Folge: Der Put Optionsschein würde um ca. 0,07 Euro auf 0,35 Euro fallen.
Wie man an dem Beispiel erkennt, kann das Delta vor allem bei der Auswahl eines Optionsscheins sehr hilfreich sein. Des Weiteren hilft die Kennzahl, um bei einem dynamischen Hedge die benötigte Anzahl der zu kaufenden Optionsscheine zu ermitteln. Je stärker der Kurs des Optionsscheins auf den Kurs des Basiswerts reagiert, desto weniger Optionsscheine sind für die Absicherung nötig.
Aber Achtung:
An dieser Stelle ist es wichtig, einige Einschränkungen zu erwähnen, um die Aussagekraft des Deltas zu relativieren. Die wichtigste Einschränkung besteht darin, dass die Kennzahl eine Momentaufnahme abbildet. Das bedeutet, dass mit ihrer Hilfe nur dann eine korrekte Aussage über die Wertentwicklung gemacht werden kann, wenn alle anderen Marktvariablen außer dem Basiswertkurs als konstant angenommen werden können. Dies wird in der Realität natürlich kaum zutreffen. Des Weiteren bleibt die Kennzahl selbst nicht konstant, sondern sie verändert sich, was mit dem sogenannten Gamma gezeigt werden kann, das wir Ihnen in der nächsten Ausgabe weiter erläutern möchten.
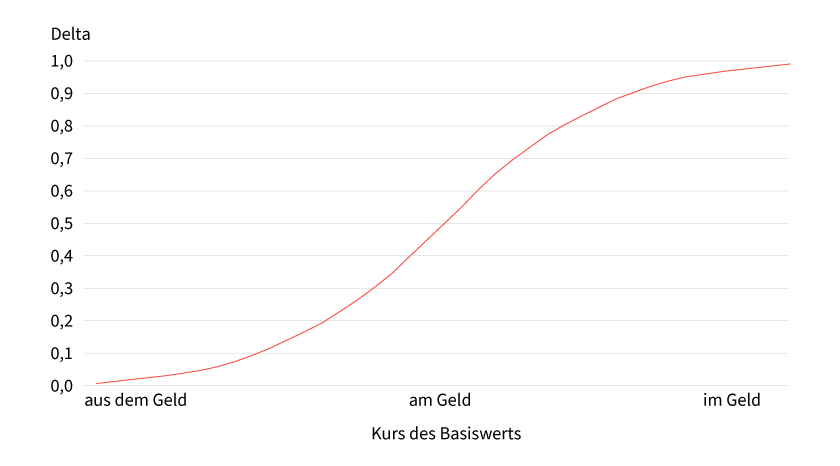
Grafik 2 zeigt den tendenziellen Verlauf des Deltas eines Call Optionsscheins in Abhängigkeit vom Kurs des Basiswerts. Je kürzer die Restlaufzeit des Optionsscheins wird, desto steiler wird der Verlauf des Deltas im Bereich »am Geld« der Kurve sein.
Weiter zu Teil 2: Gamma
Das könnte Sie auch interessieren: