Wissen
Was ist eigentlich das Rho?
Die Kennzahl Rho ist der letzte griechische Buchstabe, der im ideas-Magazin vorgestellt wird. Viele Privatanleger sind dieser Kennzahl noch nicht begegnet, da sie nicht so gebräuchlich ist wie das Delta, Vega oder Theta. Das Rho misst den Einfluss der Zinsveränderung auf den Optionspreis. Der Zinsatz wird in Prozent angegeben. Somit sagt das Rho aus, wie stark sich der Wert der Option ändert, wenn sich der risikofreie Zinssatz am Markt um 1 Prozentpunkt (100 Basispunkte) ändert (ceteris paribus, alle anderen Parameter bleiben unverändert).
Das Rho ist die erste partielle Ableitung der Black-Scholes-Optionspreisformel nach dem Zins. Für Call Optionen ist das Rho positiv, für Put Optionen negativ. Dieser Zusammenhang lässt sich intuitiv über das Auszahlungsprofil eines Optionsscheins erklären.
Falls der Basiswertkurs über dem Basispreis liegt, erhält der Inhaber einer Call Option am Laufzeitende eine Auszahlung, die der Differenz zwischen dem Basiswertkurs und dem Basispreis entspricht. Der heutige Optionspreis spiegelt die zukünftige Erwartung für die Basiswertentwicklung wider und kann als die diskontierte Erwartung der zukünftigen Auszahlung betrachtet werden. Da der Kurs des Basiswerts am Laufzeitende heute nicht bekannt ist, wird der erwartete Kurs herangezogen. In der Praxis wird dafür der Terminkurs des Basiswerts, der sogenannte Forwardkurs, betrachtet. Der Forwardkurs einer Aktie oder eines Index (angenommen es werden keine Dividenden gezahlt) errechnet sich als der aufgezinste heutige Aktien- bzw. Indexkurs:
Forward (Aktie) = Aktie x erT
Je höher der Zinssatz, umso höher ist der Forwardkurs. Der abgezinste Forwardkurs entspricht wiederum dem heutigen Aktienkurs.
r = risikoloser Zins
e = eulersche Zahl
T = Restlaufzeit der Option
Die zweite Komponente, die die erwartete Call-Auszahlung beeinflusst, ist der Basispreis, dessen heutiger Wert sich wie folgt ermittelt:
Basispreis x e–rT
Je höher der Zinssatz, umso geringer ist der abgezinste Basispreis. Die erwartete Call-Auszahlung kann so als Differenz zwischen dem Basiswertkurs und dem abgezinsten (erwarteten) Basispreis betrachtet werden. Tatsächlich lässt sich einfach beweisen (darauf wird hier verzichtet), dass der Call-Preis heute mindestens der Differenz zwischen dem Basiswertkurs und dem erwarteten Basispreis entspricht:
c ≥ Aktie – Strike x e-rT
Jetzt wird der positive Zinseinfluss auf den Call-Preis deutlich. Je höher der Zins, umso höher ist die erwartete Call-Auszahlung und umgekehrt.
Der negative Zinseinfluss auf den Put-Preis ergibt sich durch das umgekehrte Auszahlungsprofil einer Put Option. Die erwartete Auszahlung einer Put Option kann als die Differenz zwischen dem abgezinsten Basispreis und Basiswertkurs am Laufzeitende betrachtet werden. Der heutige Put-Preis ist tatsächlich jederzeit mindestens so hoch wie die genannte Differenz, das heißt:
p ≥ Basispreis x e–rT – Aktie
Daraus lässt sich der Zinseinfluss interpretieren: Je höher der Zins, umso geringer ist die erwartete Auszahlung und somit der Put-Preis.
Ein Beispiel: Ein Call auf die ABC-Aktie mit einer Laufzeit von drei Monaten und einem Basispreis von 85,00 Euro (Kurs ABC-Aktie: 84 Euro) kostet 5,56 Euro. Der 3-Monats-Zins liegt bei 0,682 Prozent p.a. Daraus ergibt sich ein Rho von 0,095. Falls sich der Referenzzins um 1 Prozentpunkt auf 1,682 Prozent p.a. erhöht, steigt der Call-Preis ceteris paribus um 9,5 Cent. Eine Zinsreduzierung um 0,25 Prozentpunkte (diese Größenveränderung ist eher am Markt üblich) würde den Optionspreis entsprechend um 2,4 Cent verringern (–0,25 x 0,095 = –0,024).
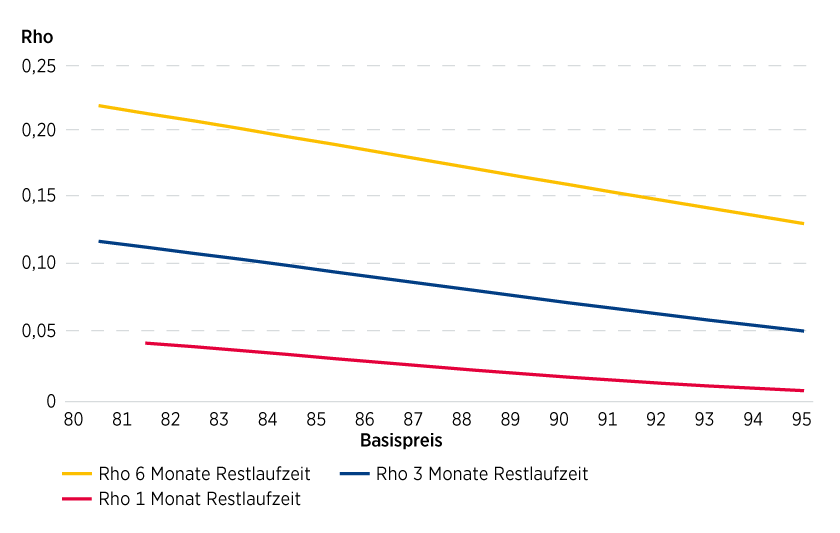
Die Grafik zeigt die Abhängigkeit des Rho vom Basispreis für Calls auf die ABC-Aktien mit jeweils drei verschiedenen Laufzeiten und bei einem Basiswertkurs von 84 Euro. Das Call-Rho fällt generell bei einem steigenden Basispreis. Weiterhin gilt: Je länger die Optionslaufzeit, desto höher ist bei einem gegebenen Aktienkurs das Rho. Am Laufzeitende ist sein Einfluss praktisch vernachlässigbar.
Das Rho hat in der Praxis die geringste Bedeutung von allen »Griechen«. Zum einen werden auf dem Terminmarkt meistens am und aus dem Geld notierende Optionen gehandelt, das heißt diejenigen mit geringerem Rho. Somit ist der Zinseinfluss nicht so stark ausgeprägt. Zum anderen kann der Rho-Einfluss über das Vega gesteuert werden, denn das Rho ist positiv korreliert mit der Volatilitätskennzahl Vega. Je geringer der Vega-Einfluss, umso geringer wird auch der Rho-Einfluss. Dennoch soll insbesondere in volatilen Marktphasen das Rho nicht ganz außer Acht gelassen werden, vor allem wenn von den Notenbanken eine Änderung der Zinspolitik erwartet wird.